MultiLayer Perceptron for Dight Recognition using PyTorch
Creating a MLP to classify digits in the MNIST dataset. The model has 5 hidden layers and uses batch normalization.
Published on: 6/8/2024
Note
The code for this project can be found on GitHub. The code is fully documented. Some images may take a while to load on this webpage.
Introduction
This post describes the multi-layer perceptron (MLP) digit classification model built, the MNIST dataset was used for our purposes. The model is implemented using the PyTorch library. The model is a feed-forward neural network with 5 hidden layers and a tanh non-linearity. The model uses batch normalization to normalize the input to each layer. The model is tested on the test set and achieves an accuracy of 97%. MLP models like this are foundational to many modern machine learning applications. They are used in Character recognition systems, Text extraction from images, Medical imaging and many more.
Background
An MLP is a neural network architecture that consists of multiple layers of neurons. Each layer produces activations that are passed onto the next layer. The final layer produces the output of the neural net. The model is trained using backpropagation and stochastic gradient descent (SGD). SGD is an optimization algorithm that is defined as follows:
Where are the weights of neurons, b is for bias and the function J is the cost function. The optimizer takes a step in the direction of the negative gradient of the loss function with respect to the parameters of the model. The learning rate determines the step size. The cost function used is negative log-likelihood, or cross-entropy loss. The cross-entropy loss is a measure of the difference between the model's predicted value and the true probability distribution. The cross-entropy loss is defined as follows:
Where the function is the model's prediction with parameters and , is the true label, and is the input to the neural network.
Implementation / Methodology
The implementation of the code is available on GitHub. Some of the main implementation details are as follows:
- The input to the neural network is a 28x28 image in batches of 32, the tensor is flattened to a 32 * 784-dimensional vector. The input is normalized by dividing by 255.0 as the maximum pixel value is 255.
def load_split_data(path, split_ratio=0.8): X, Y = torch.load(path) X = X/255 total_samples = X.size(0) training_amount = int(split_ratio * total_samples) # Split the data into training and validation sets Xtr = X[:training_amount, :, :] Ytr = Y[:training_amount] Xval = X[training_amount:, :, :] Yval = Y[training_amount:] F.one_hot(Ytr) Xtr = Xtr.view(48000,-1) Xval = Xval.view(12000,-1) return Xtr, Ytr, Xval, Yval
The function load_split_data loads the data from the path and normalizes the input. The data is then split into a training set and a validation set. The training set has 48000 samples and the validation set has 12000 samples. The labels are one-hot encoded. The input is reshaped to a 48000x784 tensor for the training set and a 12000x784 tensor for the validation set.
- Since the linear layers have 100 neurons so the first linear layer squashes 784 features to 100 and this continues for the next 4 layers. The final layer has 10 neurons, which corresponds to the number of classes in the dataset.
Batch Normalization
The following code snippet shows how batch normalization is implemented in the model.
def __call__(self,x): if self.training: xmean = x.mean(0, keepdims=True) # batch mean xvar = x.var(0, keepdims = True) # batch varience else: # use running mean and varience during inference xmean = self.running_mean xvar = self.running_var xhat = (x - xmean) / torch.sqrt(xvar + self.eps) # formula from batchnorm paper self.out = self.gamma * xhat + self.beta if self.training: with torch.no_grad(): # update running mean and varience using momentum self.running_mean = (1 - self.momentum) * self.running_mean + self.momentum * xmean self.running_var = (1 - self.momentum) * self.running_var + self.momentum * xvar return self.out
The batch normalization layer is implemented as a class. The class has a forward method that takes the input tensor x and normalizes it. The class has a training attribute that is set to True during training and False during inference. The class has a running mean and running variance that are updated during training using the momentum parameter. The class has a gamma and beta parameter that are learned during training.
Analysis
We can analyze the loss function to see how the model learns. The loss function is plotted as a function of the number of steps. The loss function is averaged over 1000 steps to reduce the noise in the plot. The plot is shown below.
plt.plot(torch.tensor(lossi).view(-1,1000).mean(1))
here lossi is a list of the log10 values of the loss function at each step.
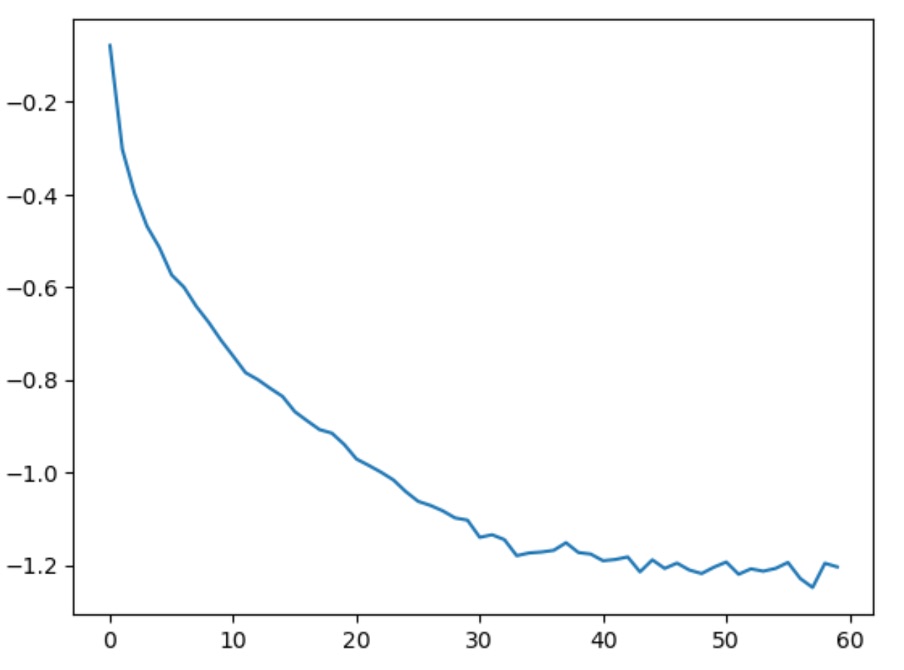
Loss Function
As the loss function illustrates the model does learn and the loss decreases over time. There is a little bit of noise in the loss function toward the end of the training, but the overall trend is a decrease in the loss function. The noise could be due to the learning rate decay, which could be too aggressive. The noise could also be due to the fact that the model is overfitting the training data.
Furthermore, when I calculated the validation loss and the training loss, I found that the validation loss was greater than the training loss. The validation loss was 0.105 and the training loss was 0.029. From this, we can infer that the model has high variance. The model is able to achieve an accuracy of 97%.
Mini Comparision
When comparing our 5-layer model to a single-layer model—which only includes a linear layer and a Tanh activation—we find that the 5-layer model can capture more complex features. For instance, when we run the test set through the single-layer model, we obtain the following results:

Single-layer network output
In the image, "P" represents the prediction made by the single-layer model, while "Label" indicates the actual value. The 28x28 images displayed correspond to these values. The single-layer model correctly classifies 7 out of 10 images, but it misclassifies 3 of them. Notably, the second-to-last image is predicted as a "6" instead of the correct label "5". However, given the ambiguity of the image, this mistake is somewhat understandable. In contrast, when we evaluate the 5-layer model on the first 10 examples from the test set (shown below), it correctly classifies all of them.

Multi-layer network output
This demonstrates that a deeper model is more capable of learning and identifying complex features, leading to improved accuracy.
Conclusion
Conclusively, the multi-layer perceptron (MLP) model for digit classification using the MNIST dataset has been successfully implemented. The model consists of 5 hidden layers and utilizes the PyTorch library for implementation. Through training and testing, the model achieves an accuracy of 97%, demonstrating its effectiveness in accurately classifying digits. Additionally, a comparison with a single-layer model highlights the superior performance of the 5-layer model in capturing complex features and improving accuracy. Overall, the MLP model proves to be a reliable and efficient approach for digit recognition tasks.